Note: An updated and condensed version of this blog is now available as one of the sections of www.MathLearningDifficulties.com
A specific math learning difficulty known as dyscalculia affects about 6% of the population. This dysfunction is of neurological origin, like dyslexia, but affects a different brain center and has its own cluster of symptoms. While it affects the same number of people as does dyslexia, unfortunately it is much less well known, so dyscalculia is frequently missed and not treated effectively.
A child has extreme difficulty learning and retrieving math "facts," such as addition and multiplication tables, or in applying techniques such as subtraction and division, or in understanding fractions.
An adult colleague, a specialist in learning disorders, reports:
I truly don't have a concept of numbers. I got through school with Bs in in algebra and trig by memorizing formulas and plugging in numbers to get answers that meant nothing to me. I can understand the mechanics of addition, subtraction, multiplication and division. Fractions take more effort... My ACT scores were all above 30 except I got 18 in math.
A high school physics student I was tutoring got an answer of 1 million meters for the wavelength of a sound wave, and had no idea that this was at all incorrect (The correct answer was 1 meter).
This math learning difficulty is due to a dysfunction of genetic/neurological origin called developmental dyscalculia, or usually just dsycalculia. Math learning difficulties or disabilities that are acquired by accident, stroke or other illness are called, in distinction, acalculia. In practice, a student with dyscalculia is defined as one who has a very difficult time learning mathematics appropriate to their age, in the absence of other causative factors such as accident, poor previous instruction, poor home environment, low IQ, or emotional illness (including math anxiety). Most often, students who are probably dyscalculic are identified by choosing among the students who fall in the lowest one-sixth of students given a standard math achievement test, but who have IQs above 80.
Dyscalculia that shows up early will be the main focus of this section, that is, dyscalculia that is diagnosable by second or third grade. At present, it is still unclear if there are forms of dyscalculia which do not cause early trouble with learning mathematics but which do cause trouble later. Further, most studies of dyscalculia have focused on children in second grade and older. A diagnosis of dyscalculia cannot reliably be made much earlier, because some symptoms of dyscalculia are normal responses at earlier ages.
SIGNS OF EARLY-ONSET DYSCALCULIA
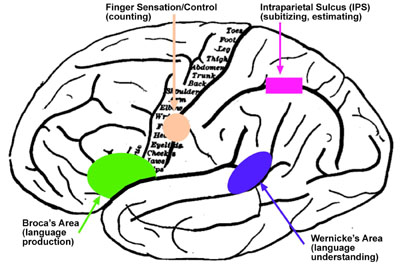
● Poor subitizing. The earliest sign that dyscalculic students have a more difficult time than their peers is in the first number task: subitizing and the associated visual counting. Subitizing is the ability to know how many of a small number of objects there are without counting them, e.g., from a brief glance. Human babies at birth have the ability to subitize, and other primates have very similiar (homologous) neural circuits: Obviously, subitizing evolved early in primate evolution (or before) because it is a survival trait. In humans, the subitizing function is located in the intraparietal sulcus (IPS) illustrated in the diagram below. Subitizing is an innate ability that does not have to be learned -- although it can be improved with training (Fischer, et al., 2008; Groffman, 2009). Children with poor subitizing appear to have difficulty with most subsequent aspects of math, detailed as follows.
● Counting to ten. The next task is that of learning to count. Children naturally learn to count on their fingers, and in fact, the brain center that is involved in counting is located in or near the brain center that provides motor control of the fingers (see Souza, 2008). This counting module is in a completely different part of the brain from the subitizing module. Dyscalculic children have a much more difficult time than their peers in understanding the process of counting and of learning "number facts" such as 4 + 3 = 7, or understanding why it is the same answer as 3 + 4.
● Learning number facts. In general, dyscalculic individuals have a much more difficult time learning and using "number facts," such as addition and subtraction, multiplication tables, etc. It is not clear whether the problem lies in the transfer to long-term memory itself, or in the ability to retrieve the appropriate item from long-term memory, i.e., using the "associative" memory function.
Educators who work with both dyslexics and dyscalculics (e.g., Cathy Davis, Director, Excelsior Academy) say that the easiest way to diagnose the existence of either condition is that the student can learn something one day, really seem to understand it well, but the next day they have forgotten it completely or at least cannot retrieve it from memory -- and this occurs in the area of their difficulty only. Repetition by itself does not seem sufficient. The dyscalculic has to relearn the same "fact" again and again, and may never be able to "learn" (access from long-term memory) some math facts. The frustration (and worse) that this causes an intelligent learner is well described in a "Letter to my Math Teacher" on the web site www.dyscalculia.org.
● Finally, estimating and counting appear to involve two different functions, the estimating ability apparently arising naturally as an extension of the subitizing function, while counting arises in the finger motor control area. Dyscalculics are notably poor at estimating, e.g., knowing when a math answer makes sense, etc.
ORIGIN IN BRAIN "NUMBER MODULE"
There is evidence that the primary neural deficit that causes dyscalculia lies in a specific number module (Butterworth, 2005). Adding the evidence contributed by Fischer et al. (2008) leads to the conclusion that the specific number module affected must involve the subitizing function. The way that a basic dysfunction in subitizing (and visual counting) could lead to the other symptoms of dyscalculia is as follows. Learning to understand, count and add small numbers efficiently requires the use of an effective subitizing (visualizing) function (see Benoit, et al., 2004). This would explain why dyscalculics have such a difficult time with this task.
There is evidence that the primary neural deficit that causes dyscalculia lies in a specific number module (Butterworth, 2005). Adding the evidence contributed by Fischer et al. (2008) leads to the conclusion that the specific number module affected must involve the subitizing function. The way that a basic dysfunction in subitizing (and visual counting) could lead to the other symptoms of dyscalculia is as follows. Learning to understand, count and add small numbers efficiently requires the use of an effective subitizing (visualizing) function (see Benoit, et al., 2004). This would explain why dyscalculics have such a difficult time with this task.
The next step, as Sousa (2008) suggests, is learning the mental number line, seeing numbers from small to large arranged along a line. This requires a combination of the subitizing and counting functions, which is potentially problematic even for normal learners because the two centers are separated by a large distance in the brain. For dyscalculics, who have difficulty with both counting and subitizing, it would seem to be doubly difficult to obtain a good sense of the mental number line.
A deficit in the subitizing module therefore explains well the main difficulties of the dyscalculic student at the early stages. In addition, Butterworth, et al. (2011) note that, with typical learners, the number module is routinely accessed even during the routine task of retrieving simple arithmetic facts from memory. Therefore, because the function of the number module is disturbed in dyscalculics, they have (much) more difficulty learning and remembering simple arithmetic facts than do typical learners.
In support of the subitizing-deficit conclusion, we note that about 6% of all students have dyscalculia according to present estimates. This is very nearly the same as estimates for the fraction of students with dyslexia, defined similarly to dyscalculia but with regard to reading and other language difficulties. These two groups overlap: about 60% of students with either condition have both. It is also true that dyslexic students, because of trouble with language, will have some characteristic difficulties with learning mathematics.
However, it has recently been convincingly shown that the symptoms caused by (at least early) dyscalculia and those caused by dyslexia do not overlap. The two conditions appear to not have the same neurological cause, and they are additive in their effects (Landerl, et al., 2009). This finding supports the conclusion that dyscalculia involves a dysfunction in a specific number module. Combined with the findings by Fischer, et al., we come to the tentative conclusion that the dysfunction at least must involve the subitizing part of the number module.
The situation as it now stands is illustrated with the diagram to the left, which shows that only three genes or genetic factors (A, B, C) are necessary to explain the observations (although of course the actual genetic cause may be much more complicated). To make the numbers simple, we assume that 8% of the population have dyscalculia, and the same fraction have dyslexia. The total affected is not 16%, however, because of overlap. We assume, consistent with the data, that 5 of every 8 people (62.5%) with either condition have both conditions (middle group at bottom of diagram).
The diagram suggests that the conclusions of many of the earlier studies have to be regarded with care because many of these studies did not test independently for reading problems and so they were actually studying a mixed group, comprised of the two groups on the left. It is not surprising that their conclusions were consequently complex. In contrast, Landerl, et. al. (2009) did divide their subject population into the three groups, and found the results much easier to understand. It is also interesting that the proportions of subjects in the three groups in their study were in the ratios suggested by the figure -- even though their selection criteria was simply based on math and reading scores.
The crucial importance of good subitizing in normal development was shown in a longitudinal study in a random group of first graders. Penner-Wilger, et al., 2007) measured three components suspected of importance in the subsequent development of arithmetic skills: Subitizing ability, finger sensitivity (gnosia) and finger motor control (finger tapping facility). They then measured the subsequent development of number system knowledge (understanding numbers, counting, cardinality, etc.) and calculation skill (knowing and using math facts accurately). The diagram on the left shows their main conclusions, with the width of the arrow lines illustrating the main connections.
Good subitizing ability contributed independently to number system knowledge AND calculation skill (see the two arrows). In contrast, the systems associated with learning counting (finger skills) contributed directly only to number system knowledge, which subsequently had a strong effect on calculation skill, as would be expected. Even though subitizing has no obvious connection with learning math facts, therefore, this research illustrates that there is an important connection independent of subitzing's direct effect on basic number system understanding.
Finally, a recent NIH report confirms these findings, summarizing a study by Mazzocco, et al. (2011). They report that a deficit in the subitizing/estimating module was very common in students who consistently tested in the lowest 10% in math achievement. However, there was no such correlation for those students in the next lowest group, those testing in the 11 to 25% range. This fits in with our view that there are several different reasons for math learning difficulties, that a deficit in the subitizing/estimating module underlies those having the most difficulty, and this comprising about 6% of the population.
However, it has recently been convincingly shown that the symptoms caused by (at least early) dyscalculia and those caused by dyslexia do not overlap. The two conditions appear to not have the same neurological cause, and they are additive in their effects (Landerl, et al., 2009). This finding supports the conclusion that dyscalculia involves a dysfunction in a specific number module. Combined with the findings by Fischer, et al., we come to the tentative conclusion that the dysfunction at least must involve the subitizing part of the number module.The situation as it now stands is illustrated with the diagram to the left, which shows that only three genes or genetic factors (A, B, C) are necessary to explain the observations (although of course the actual genetic cause may be much more complicated). To make the numbers simple, we assume that 8% of the population have dyscalculia, and the same fraction have dyslexia. The total affected is not 16%, however, because of overlap. We assume, consistent with the data, that 5 of every 8 people (62.5%) with either condition have both conditions (middle group at bottom of diagram).
The diagram suggests that the conclusions of many of the earlier studies have to be regarded with care because many of these studies did not test independently for reading problems and so they were actually studying a mixed group, comprised of the two groups on the left. It is not surprising that their conclusions were consequently complex. In contrast, Landerl, et. al. (2009) did divide their subject population into the three groups, and found the results much easier to understand. It is also interesting that the proportions of subjects in the three groups in their study were in the ratios suggested by the figure -- even though their selection criteria was simply based on math and reading scores.
The crucial importance of good subitizing in normal development was shown in a longitudinal study in a random group of first graders. Penner-Wilger, et al., 2007) measured three components suspected of importance in the subsequent development of arithmetic skills: Subitizing ability, finger sensitivity (gnosia) and finger motor control (finger tapping facility). They then measured the subsequent development of number system knowledge (understanding numbers, counting, cardinality, etc.) and calculation skill (knowing and using math facts accurately). The diagram on the left shows their main conclusions, with the width of the arrow lines illustrating the main connections.
Good subitizing ability contributed independently to number system knowledge AND calculation skill (see the two arrows). In contrast, the systems associated with learning counting (finger skills) contributed directly only to number system knowledge, which subsequently had a strong effect on calculation skill, as would be expected. Even though subitizing has no obvious connection with learning math facts, therefore, this research illustrates that there is an important connection independent of subitzing's direct effect on basic number system understanding.
Finally, a recent NIH report confirms these findings, summarizing a study by Mazzocco, et al. (2011). They report that a deficit in the subitizing/estimating module was very common in students who consistently tested in the lowest 10% in math achievement. However, there was no such correlation for those students in the next lowest group, those testing in the 11 to 25% range. This fits in with our view that there are several different reasons for math learning difficulties, that a deficit in the subitizing/estimating module underlies those having the most difficulty, and this comprising about 6% of the population.
BRAIN TRAINING CAN IMPROVE MATH PERFORMANCE
In their review, Butterworth et al. (2011) note that the typical educational approach to helping dyscalculics focuses on remedial work to fill in their conceptual and operational gaps, e.g., using various techniques to help them learn and retrieve arithmetic facts. These techniques usually include lots of repetition, which is stressful for the student and time consuming of teacher and special educator's time. They suggest, "In contrast, neuroscience research suggests that rather than address isolated conceptual gaps, remediation should build the foundational number concepts first." They go on to review several software programs designed to do this. However, they do not, for some reason, include the most obvious, the direct training of subitizing as discussed next.
The possibility that subitzing practice can help dyscalculics is derived from other results reported in Fischer's papers. They demonstrated that even a small amount of training in subitizing improved the ability of the (probably dyscalculic) children to subitize, and showed this subitizing improvement resulted in a significant increase in mathematics ability!
The papers report that students were given small portable instruments to take home to practice subitizing on. The software started with identification of small numbers of objects, consistent with the students' initial abilities, but then increasing numbers were shown as ability increased. Students were trained on the machine for three weeks at 15 minutes per day. Software in the machine allowed the study directors to verify the amount of training, to monitor the individual student's improvement and to adjust the software appropriately.
After only three weeks of training, the dyscalculic students subitizing ability improved sufficiently that they now tested, on average, in the normal range. More important, their scores on a standard mathematics test showed a small (but significant) improvement after even this short a time. Most important, following the training, the dyscalculic student math scores continued to improve in the classroom for the following year with only normal mathematics instruction. A year later, Fischer reports (personal communication) that the math skills of students who had been treated with the subitizing practice (for only three weeks) had continued to improve compared to students who had not gotten the training. This included learning math facts!
In other words, the subitizing training allowed the students to improve in areas of mathematics which are not at all obviously related to the ability to subitize. This seems to me to be convincing proof that the core deficit common to (at least) early-onset dyscalculia is a defect in the subitizing module.
If you have a young child who is showing signs of dyscalculia, I think it would certainly be reasonable to make the minimal investment required for several weeks practice with subitizing. Further information on access to available programs is discussed below.
In their review, Butterworth et al. (2011) note that the typical educational approach to helping dyscalculics focuses on remedial work to fill in their conceptual and operational gaps, e.g., using various techniques to help them learn and retrieve arithmetic facts. These techniques usually include lots of repetition, which is stressful for the student and time consuming of teacher and special educator's time. They suggest, "In contrast, neuroscience research suggests that rather than address isolated conceptual gaps, remediation should build the foundational number concepts first." They go on to review several software programs designed to do this. However, they do not, for some reason, include the most obvious, the direct training of subitizing as discussed next.
The possibility that subitzing practice can help dyscalculics is derived from other results reported in Fischer's papers. They demonstrated that even a small amount of training in subitizing improved the ability of the (probably dyscalculic) children to subitize, and showed this subitizing improvement resulted in a significant increase in mathematics ability!
The papers report that students were given small portable instruments to take home to practice subitizing on. The software started with identification of small numbers of objects, consistent with the students' initial abilities, but then increasing numbers were shown as ability increased. Students were trained on the machine for three weeks at 15 minutes per day. Software in the machine allowed the study directors to verify the amount of training, to monitor the individual student's improvement and to adjust the software appropriately.
After only three weeks of training, the dyscalculic students subitizing ability improved sufficiently that they now tested, on average, in the normal range. More important, their scores on a standard mathematics test showed a small (but significant) improvement after even this short a time. Most important, following the training, the dyscalculic student math scores continued to improve in the classroom for the following year with only normal mathematics instruction. A year later, Fischer reports (personal communication) that the math skills of students who had been treated with the subitizing practice (for only three weeks) had continued to improve compared to students who had not gotten the training. This included learning math facts!
In other words, the subitizing training allowed the students to improve in areas of mathematics which are not at all obviously related to the ability to subitize. This seems to me to be convincing proof that the core deficit common to (at least) early-onset dyscalculia is a defect in the subitizing module.
If you have a young child who is showing signs of dyscalculia, I think it would certainly be reasonable to make the minimal investment required for several weeks practice with subitizing. Further information on access to available programs is discussed below.
It seems possible that older students and adults with dyscalculia might be helped with such a program as well.
PROGRAMS FOR SUBITIZING IMPROVEMENT
● In the United States, S. Groffman has developed a subitizing practice program, SUB iNet, produced by Home Therapy Systems. It runs on both Windows and Mac.
This program is straightforward and well-designed. The student is taken through a series of symbols flashed on a screen for short time, and told if their answer is correct. The program starts with one or two symbols and increases slowly in difficulty as the student's improvement allows. A young child would have to be instructed on how to use the program initially but should be able to proceed on their own after that. It does not have a childish game to contend with, so it would be suitable for people of any age to use. However, this can be a drawback with young children, as they may need adult encouragement to persist in practicing for the 15 minutes a day required. However, of those available, this program would be my first recommendation for serious work on the improvement of subitizing for a person of any age with dyscalculia. This program is available through optometrists and other qualified professionals.
It seems to me that there is a significant problem with the screening test included in this program. This screening test flashes a number of objects on the screen for 0.2 seconds and the student then reports the number seen. Each number of objects (one to six) is shown twice in random order, so a perfect score equals 12 correct responses. While the test does keep track of the average time for the response, it does not use this information effectively. Rather, the pass/fail criterion is only based on the total number correctly identified out of 12 presentations. This is a significant problem because, as Fischer et al. (2008) clearly show, their test subjects (poor math students) have two problems with their subitizing/visual counting function: accuracy AND speed of response. For example, for the case with five items presented, on average the test subjects got the number of items correct 80% of the time, while the controls did only slightly better at 90% correct. The average response time of the controls was 2.0 seconds for this same number of objects, compared to 2.6 seconds for the test subjects (these reactions times include only correct responses).
My reasons for this concern come from recent experience field-testing this program: I have used the pass/fail screen on some students who are clearly early-onset dyscalculic (based on other symptoms and history) but who appear to be able to use a good visual memory to make up for their (probable) deficiency in subitizing. (This is exactly what one student spontaneously reported doing!) That is, some students with probable dyscalculia could score a perfect 12 on the screening test but take longer than average to respond due to having to visually count all of the objects. In contrast, a person with good subitizing ability does not have to visually count the items in their subitizing range, so a normal person will respond faster on average. However, the average response time for normal children was not reported for this screening test so only the total correct is made available for evaluation.
My tentative conclusion is that this program is still the best available for practicing subitizing but that the screening test it contains should not be used alone to determine who is a potential subject for the training: The screening test results are useful but the information is incomplete, a decision on using the training program must be supplemented by a careful history of symptoms (as described above).
● An adaptive game for dyscalculic children has recently been developed: Number Bonds is now available at www.number-sense.co.uk/numberbonds/. It is played online. It is obviously still in development, as it does not really tell the student what to do. It is, however, easy enough to figure out.
The sequence of screens includes colored even rods (shown), colored odd rods, then colored both; followed by similar sequences with uncolored rectangles and then rectangles labeled with a number giving their correct length, both colored and blank; and finally numbers appear without bars. The object of the program is to teach number sense, the connection between the number and the length it represents, and to drive home the concept of commutivity. As illustrated, the top two bars in the stack demonstrate physically how 8+2 = 2+8. Also, the program obviously allows repeated concrete practice of the math facts for the number pairs adding to ten.
● The Number Race is a free open-source software program available online. It is currently available to run on Windows 2000, XP, and Vista. It is available in a number of languages and has a variety of modules intended to teach early number concepts. It is intended for children aged 4-8 years, and engages the child by asking him or her to play a simple game. This is probably useful for children of that age range but would potentially get in the way of practice by older students or adults. Also, this program does not specifically include subitizing practice, but does include lots of practice in comparing sizes of numbers, etc.
● In Europe, B. Fischer has developed a network of partner institutions who offer diagnosis, followed by training using stand-alone portable devices to be used at home. The diagnostic procedure used not only checks subitizing ability but eye movement abilities required to read and do math.
B. Butterworth, S. Varma, D. Laurillard, "Dyscalculia: From brain to education," Science, 232, 1049-1053 (May 27, 2011). An excellent recent review article, includes a review of computer programs for helping dyscalculic children. They recommend, in general, that such programs be used developed and used extensively in educating these children in place of more costly methods, e.g., special needs teachers using physical manipulatives such as Cuisenaire rods, etc.
L. Benoit, H. Lehalle, F. Jouen, "Do Young Children Acquire Number Words Through Subitizing or Counting?" Cognitive Develop., 19 (2004). They conclude that subitizing is required "for acquiring the meaning of the first few number words."
B. Butterworth, "Developmental Dyscalculia," in Handbook of Mathematical Cognition, J. Campbell (Ed) 455-467 (2005).
L. Benoit, H. Lehalle, F. Jouen, "Do Young Children Acquire Number Words Through Subitizing or Counting?" Cognitive Develop., 19 (2004). They conclude that subitizing is required "for acquiring the meaning of the first few number words."
B. Butterworth, "Developmental Dyscalculia," in Handbook of Mathematical Cognition, J. Campbell (Ed) 455-467 (2005).
J. Emerson, P. Babtie, The Dyscalculia Assessment (2010) . An instruction manual for a detailed assessment of dyscalculia and other math difficulties including suggestions for interpreting and using the assessment to plan the intervention strategy. Primarily for grade school children of normal intelligence having particular difficulty with math, intended for teachers and other special needs professionals.
B. Fischer et al., "Subitizing and Visual Counting in Children with Problems in Acquiring Basic Arithmetic Skills," Optometry & Visual Develop., 39, 24-29 (2008).
B. Fischer et al., "Effects of Daily Practice on Subitizing, Visual Counting, and Basic Arithmetic Skills," Optometry & Visual Develop., 39, 30-34 (2008).
S. Groffman, "Subitizing: Vision Therapy for Math Deficits," Optometry & Vision Develop., 40, 229-238 (2009).
K. Landerl et al., "Dyslexia and dyscalculia: Two learning disorders with different cognitive profiles," J. Exper. Child Psychol., 103, 309-324 (2009).
N. Penner-Wilge, L. Fast, J. LeGevre, B. Smith-Chant, S. Skwarchuk, D. Kamawar, J. Bisan, "The foundations of numeracy: Subitizing, finger gnosia, and fine motor ability," conference proceedings archive, PDF (2007).
D. Sousa, How the Brain Learns Mathematics (2008).
N. Penner-Wilge, L. Fast, J. LeGevre, B. Smith-Chant, S. Skwarchuk, D. Kamawar, J. Bisan, "The foundations of numeracy: Subitizing, finger gnosia, and fine motor ability," conference proceedings archive, PDF (2007).
Dyscalculia.org is a very useful web site devoted to math learning disabilities, with moving personal reports from those suffering from the condition.
The website for the National Center for Learning Disabilities is an excellent resource for all learning difficulties.
The Learning Disabilities Association of America conducts an annual conference open to public and professionals that contains (a small proportion of) sessions devoted to dyscalculia.
All-Ways Learning, by Dr. Dawn Romano, offers full service assistance to those with learning disabilities in the New Orleans area.
All-Ways Learning, by Dr. Dawn Romano, offers full service assistance to those with learning disabilities in the New Orleans area.
ADDITIONAL INFORMATION ON IMPORTANT RESEARCH REPORTS and COMMENTS
